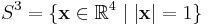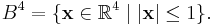Slice knot

A slice knot is a type of mathematical knot. It helps to remember that in knot theory, a "knot" means an embedded circle in the 3-sphere

$S^3 = \{\mathbf{x}\in \mathbb{R}^4 \mid |\mathbf{x}|=1 \}$

and that the 3-sphere can be thought of as the boundary of the four-dimensional ball

$B^4 = \{\mathbf{x}\in \mathbb{R}^4 \mid |\mathbf{x}|\leq 1 \}.$

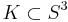A knot $K\subset S^3$ is slice if it bounds a nicely embedded disk D in the 4-ball.

What is meant by "nicely embedded" depends on the context, and there are different terms for different kinds of slice knots. If D is smoothly embedded in B⁴, then K is said to be smoothly slice. If K is only locally flat (which is weaker), then K is said to be topologically slice.

Any ribbon knot is smoothly slice. An old question of Fox asks whether every slice knot is actually a ribbon knot.

The signature of a slice knot is zero.

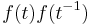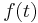The Alexander polynomial of a slice knot factors as a product $f(t)f(t^{-1})$ where $f(t)$ is some integral Laurent polynomial. This is known as the Fox–Milnor condition.

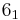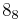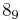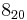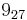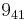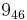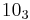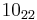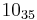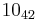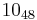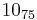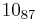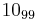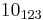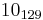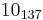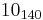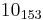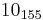The following is a list of all slice knots with 10 or fewer crossings; it was compiled using the Knot Atlas: $6_1$ , $8_8$ , $8_9$ , $8_{20}$ , $9_{27}$ , $9_{41}$ , $9_{46}$ , $10_3$ , $10_{22}$ , $10_{35}$ , $10_{42}$ , $10_{48}$ , $10_{75}$ , $10_{87}$ , $10_{99}$ , $10_{123}$ , $10_{129}$ , $10_{137}$ , $10_{140}$ , $10_{153}$ and $10_{155}$ .